
이번 포스팅에서는 다중 분류, 즉 분해야 할 클래스의 개수가 3개 이상일 때의 예측 모델을 만드는 법에 대해 말해보겠다.
이전 포스팅을 떠올려보면, 마지막 출력층의 활성함수를 시그모이드 함수로 설정 + BCE 손실함수를 채택함으로써 이진 분류를 수행하는 모델을 만들었었다.
당시에 '피곤하다'는 1의 클래스를 부여하고, '피곤하지 않다'는 0의 클래스를 부여하여 이진 분류를 수행하였다.
그렇다면 분류할 클래스가 3개(사과,배,귤)인 예측 모델을 만들고 싶다면 어떻게 해야할까?
사과, 배, 귤을 각각 0,1,2 로 맵핑하면 될까?
그렇지 않다. 사과일 확률이 0.4, 배일 확률이 0.1, 귤일 확률이 0.5인 데이터가 들어왔을 때를 예로 들면, 0과 2사이인 1에 가까운 값이 최종 출력되어 해당 객체를 배라고 최종 예측하게 된다.
이러한 문제를 해결하기 위해 원-핫 인코딩(one-hot encoding)이라는 방법이 사용된다.
사과, 배, 귤을 각각 [ 1 0 0 ], [ 0 1 0 ], [ 0 0 1 ] 의 벡터로 맵핑하여 학습을 진행시키면, 위와 같이 [ 0.4, 0.1, 0.5 ] 의 출력이 나왔을 때 확률값이 가장 높은 귤을 제대로 예측해낼 수 있다.
다중분류에서 마지막 층에서의 활성함수로 자주 사용되는 소프트맥스(softmax)에 대한 소개를 하겠다.

식을 살펴보면 클래스별 확률을 모두 더한 값이 1이 된다.
이제 손실함수를 설정해 주어야 한다. 다중 분류에서는 CE(cross entropy) loss를 사용한다.

Binary cross entropy 손실함수의 원리와 같으나 항이 클래스의 개수만큼 생긴다고 보면 된다.
정답에 해당하는 항만 남게되고, 이 항의 예측값(y_hat)의 크기를 크게(1에 가깝게) 만드는 것이 목적이다.
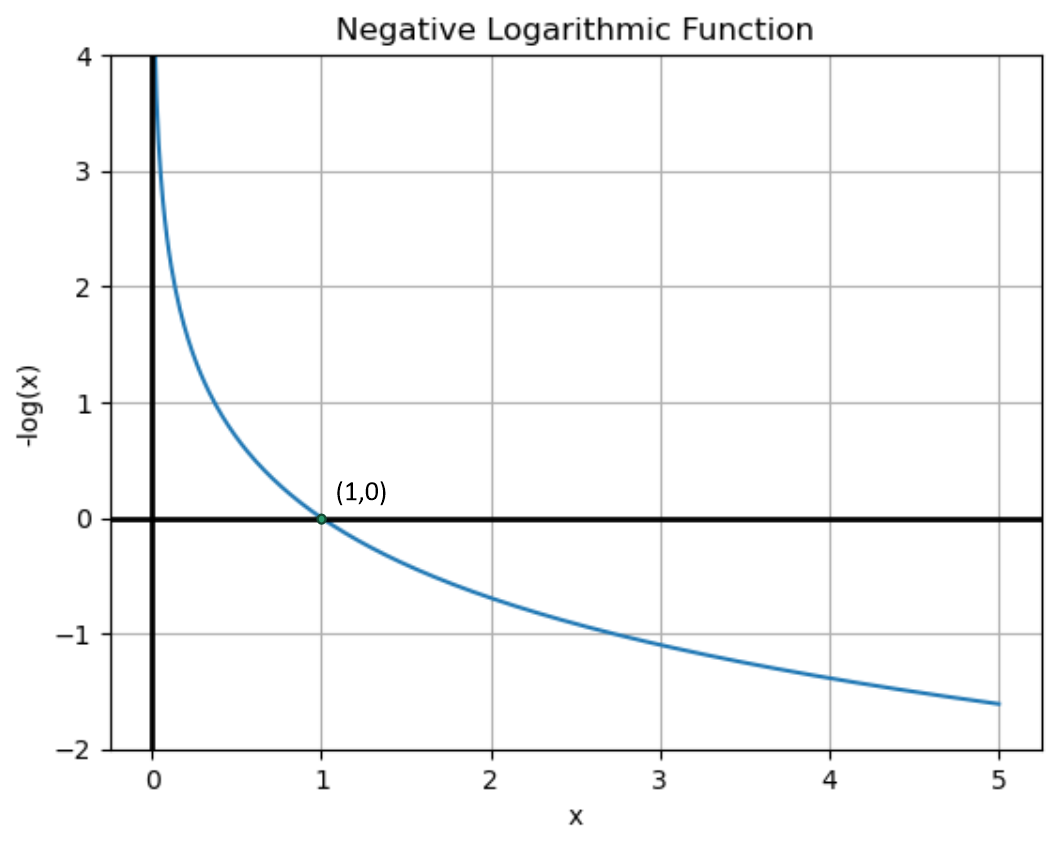
예측값의 크기는 확률이므로 0~1 사이의 값이 될 것이다. 1에 가까워질 수록 함수값이 작아지므로 -log함수를 최소화하기 위해서는 예측값(y_hat)을 가능한 1에 가깝게 만들어 주어야 한다.
모델의 마지막 층의 활성함수로 소프트맥스 함수를 채용하고 CE 손실함수를 설정하여 다중분류 모델을 만들 수 있다.
'딥러닝 기초이론' 카테고리의 다른 글
| [딥러닝 기초이론6] 과적합(overfitting)과 로컬 미니멈(local minimum) (5) | 2024.03.16 |
|---|---|
| [딥러닝 기초이론4-1] 데이터의 특성 증가와 활성함수 (3) | 2024.03.13 |
| [딥러닝 기초이론4] 로지스틱 회귀 (logistic regression) (1) | 2024.03.13 |
| [딥러닝 기초이론3-2] 미니 배치 학습(mini-batch learning)과 텐서(Tensor) (4) | 2024.03.13 |
| [딥러닝 기초이론3-1] 복잡한 신경망에서의 그라디언트 (Backpropagation) (2) | 2024.03.12 |