
지금까지 선형 회귀 분석을 통해 주어진 학습 데이터를 잘 대표하는 직선의 방정식을 찾고, 이를 이용해서 새로운 입력값에 대한 결과를 예측해보았다.
하지만 이번에는 조금 다른 문제를 다뤄보겠다. 주어진 입력에 대해서 예측이 그렇다 or 아니다 두가지 중 하나로 결정되는 문제이다.
수면시간에 따른 피로도를 예측하는 대신, 수면시간에 따라서 피곤하다 or 피곤하지 않다로 분류되는 경우이다.
| 수면시간(h) | 1 | 3 | 5 | 7 | 9 |
| 피로도(%) | 100 | 75 | 60 | 25 | 15 |
| 피곤한지 여부 | O | O | O | X | X |
1,3,5 시간 수면 후 피곤하다, 7,9시간 수면 후 피곤하지 않다는 데이터를 가지고 이진분류를 수행하는 예측 모델을 만들어보겠다.
피곤하다를 1로 맵핑하고 피곤하지 않다를 0으로 맵핑해서 좌표평면위에 표현하면 다음과 같을 것이다.
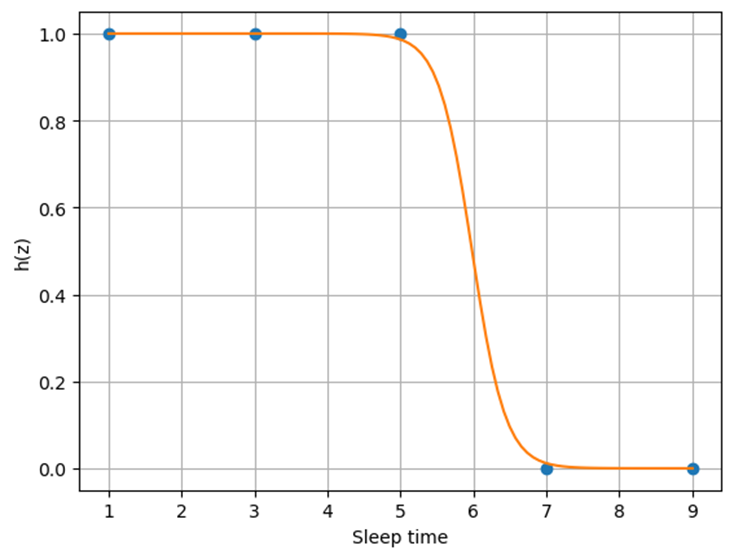
이러한 출력 결과를 얻으려면 최종 출력이 0~1의 값으로 나오게 만들어야 한다.
이를 위해 시그모이드 함수가 활용된다.
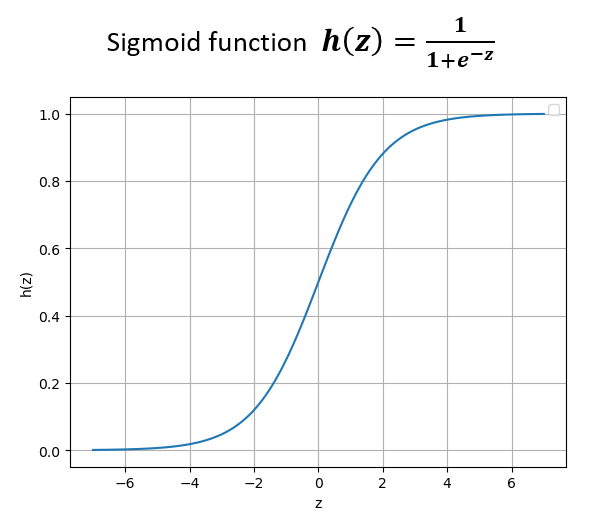
시그모이드 함수의 입력 z가 음의 무한대라면 함수값 h(z)=0 이고, 입력 z가 양의 무한대라면 함수값 h(z)=1 이다.
선형연산으로 얻어진 값 z에 시그모이드 함수를 통과시키면 그 출력이 0~1의 값으로 제한된다.
이와 같이 선형연산으로 얻어진 값을 목적에 따라 통과시키는 함수를 활성함수(activation function)이라고 부른다.
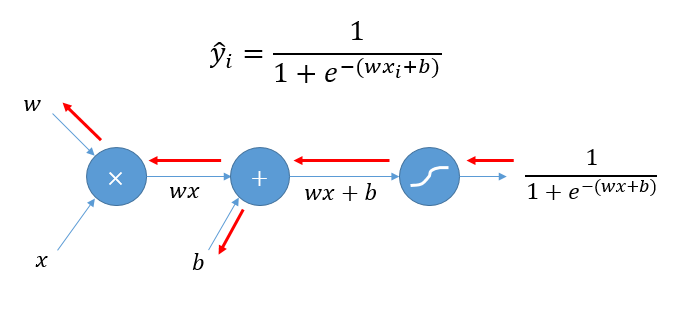
선형 연산 후 활성화 함수를 거치는 과정을 도식화해보면 다음과 같다.
여기서 끝이 아니다. 이진분류에 적합한 손실함수를 설정해주어야 한다.
여태까지는 선형회귀에서 사용되는 MSE 손실함수를 최소화하는 방법으로 최적화를 진행하였다.
그러나 생각해보면, 이진분류는 오차의 제곱으로는 그 정확도를 잘 대변한다고 보기는 어렵다.
그러므로 이진분류에 적합한 손실함수를 설정하여 최적화를 진행하여야 한다.
이진분류에서는 BCE loss (binary cross entropy loss)라는 손실함수가 사용된다.
BCE loss는 다음 두가지를 고려한다.
1. 정답이 1일 때는 예측값이 1에 가까울 수록 학습 오차가 작다.
2. 정답이 0일 때는 예측값이 0에 가까울 수록 학습 오차가 작다.

이를 수식으로 바꿔보면 다음과 같다. 최대화 해야 하는 목적함수에서 negative를 해주어 손실함수로 만들어주고 최적화를 편리하게 하기 위해 log를 씌워 합의 함수로 만든다.

-log함수의 정의역이 되는 부분은 예측모델이 산출하는 확률이고, [0,1]이라는 것에 동의할 수 있을 것이다.
x가 1에 가까울수록 (정답에 가까워질수록) 함수값이 최소화되는 것을 확인할 수 있다.
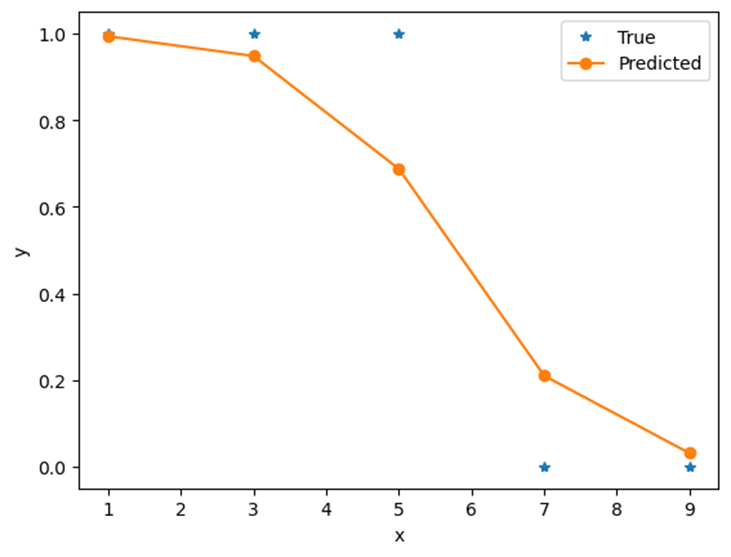
'True' 데이터를 활용해 만든 예측 모델('Predicted')이다. 설계한대로 1부터 0까지의 수치가 출력됨을 알 수 있다.
출력값에서 반올림을 하여 1또는 0으로 바꿔주고, 최종 출력이 1이라면 피곤하다, 0이라면 피곤하지 않다는 예측을 할 수 있다.
'딥러닝 기초이론' 카테고리의 다른 글
| [딥러닝 기초이론5] 다중 분류(Multi-class classification) (0) | 2024.03.16 |
|---|---|
| [딥러닝 기초이론4-1] 데이터의 특성 증가와 활성함수 (3) | 2024.03.13 |
| [딥러닝 기초이론3-2] 미니 배치 학습(mini-batch learning)과 텐서(Tensor) (4) | 2024.03.13 |
| [딥러닝 기초이론3-1] 복잡한 신경망에서의 그라디언트 (Backpropagation) (2) | 2024.03.12 |
| [딥러닝 기초이론3] 인간의 신경계를 모티브로 한 인공신경망 (6) | 2024.03.06 |