지금까지는 데이터의 한가지 요소(수면 시간)를 보고 원하는 데이터(피로도)를 예측하는 모델을 만들었다.
하지만 고려해야 할 요소가 한가지가 아니라면 어떻게 해야할까?
고려사항이 추가된 문제를 선형회귀의 관점에서 살펴보겠다.
| 수면시간(h) | 1 | 3 | 5 | 7 | 9 |
| 기온(°C) | 30 | 29 | 28 | 24 | 25 |
| 피로도(%) | 100 | 75 | 60 | 25 | 15 |
이 표를 보면, 기온이라는 요소가 추가되었다.
이제 이 데이터셋을 사용하여 수면시간과 기온 두가지 요소를 고려하여 피로도를 예측하는 모델을 만들어보려고 한다.
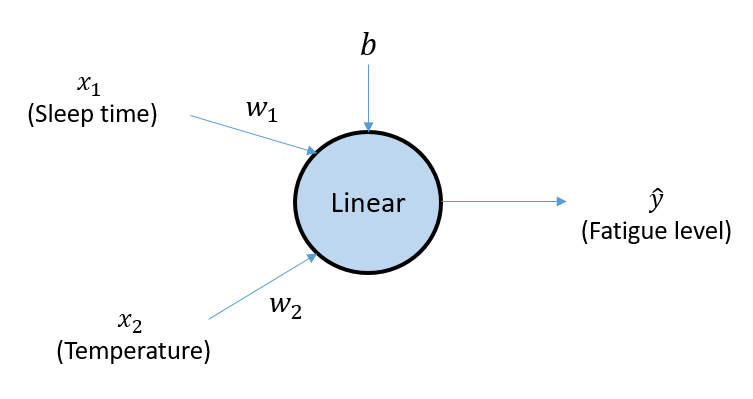
이 경우 그림과 같이 추가적으로 기온이 변수로 들어가서 선형연산에 포함된다.

행렬연산식을 보면 위와 같다.
이는 수면시간과 기온을 고려하여 피로도를 측정하는 예측 모델로, 3차원 공간 상에 그림과 같이 나타낼 수 있다.

한가지 요소만을 고려하여 만들어진 2차원 공간에서의 직선 예측모델과 다르게, 예측 모델로 3차원 공간 안에서의 평면이 생성되었음을 알 수 있다.
다음으로 활성함수에서 생기는 문제를 잠깐 짚고 넘어가겠다.

다음과 같이 활성함수로 시그모이드 함수를 쓰며 다수의 층으로 연결된 딥러닝 모델에서 생기는 문제가 있다.
[딥러닝 기초이론3-1] 에서, 인공신경망은 역전파과정을 진행시키며 그라디언트를 계산하고 파라미터들을 업데이트한다.
그러나 위와 같이 층수가 많아지다 보면 기울기 소실(vanishing gradient) 문제가 발생하게 된다.

그래프에서 파란색은 시그모이드 함수이고, 노란색 점선 그래프는 시그모이드를 미분한 함수이다.
[딥러닝 기초이론3-1] 에서 보았듯이 각 노드에서의 그라디언트가 계속해서 곱해지며 최종 편미분 값을 산출하게 되는데, 시그모이드를 미분한 값은 기껏해야 0.25가 최대값이다.
1보다 작은 이 값이 역전파 과정에서 계속 곱해지게 된다면? 그렇다, 입력부에 도착했을때는 0에 가까운 아주 작은 값이 남아있게 될 것이고, 이것은 유의미한 파라미터 업데이트를 만들어낼 수 없다.
하지만 그렇다고 해서 활성함수로 선형함수를 채용하면 깊은 층을 쌓는 이유가 없어진다.

그래서 ReLU(Rectified Linear Unit)함수가 자주 사용되는데 정확한 이유는 설명하기 어려우나 현재로서 가장 성능이 뛰어나다고 볼 수 있는 활성함수 중 하나이다.

x>0인 구간에서는 출력을 0으로 만들어 비선형성을 확보하고, x>0인 구간에서는 기울기가 1인 함수이다. 따라서 기울기 소실문제와 선형성 문제를 모두 해결이 가능하다.
ReLU를 살짝씩 바꾸어 만든 함수들도 종류가 다양하며, 자주 사용된다.
'딥러닝 기초이론' 카테고리의 다른 글
| [딥러닝 기초이론6] 과적합(overfitting)과 로컬 미니멈(local minimum) (5) | 2024.03.16 |
|---|---|
| [딥러닝 기초이론5] 다중 분류(Multi-class classification) (0) | 2024.03.16 |
| [딥러닝 기초이론4] 로지스틱 회귀 (logistic regression) (1) | 2024.03.13 |
| [딥러닝 기초이론3-2] 미니 배치 학습(mini-batch learning)과 텐서(Tensor) (4) | 2024.03.13 |
| [딥러닝 기초이론3-1] 복잡한 신경망에서의 그라디언트 (Backpropagation) (2) | 2024.03.12 |